- Caractéristiques physiques et évolution des différents prototypes
- Mesures magnétiques
- Système de mesure
- Evolution du champ magnétique en fonction de la fréquence
- Evolution de l'induction en fonction de la fréquence
- Perméabilité magnétique
- Mesures mécaniques
- Optimisation du point de fonctionnement
- Influence du champ statique
- Influence de la pré-contrainte
- Mesures de déplacement Mode libre
- Mise en évidence du doublement de fréquence
- Déplacement en fonction de la pré-contrainte
- Déplacement en fonction de la fréquence
- Comparaison entre les deux méthodes de mesure du déplacement
- Mesure de distorsion harmonique du déplacement (THD)
- Influence de la fréquence sur l'hystérésis
- Diagramme de Bode : accélération en fonction du courant d'alimentation
- Mesures de force
- Mode bloqué, mesures de force
- Force développée en fonction des différentes précontraintes
- Force développée pour différentes fréquences
- Taux de distorsion harmonique de la force
- Influence de la structure de blocage pour la mesure de force
Prototype |
N░1 |
N░4 |
Poids (kg) |
2.05 |
4 |
Dimension (mm) |
H=150, l=50,L=110 |
H=150, l=100, L=100 |
Inductance (H) |
52.10-6 |
4,08 |
Résistance du bobinage (W ) |
15.10-3 |
1,08 |
Diamètre du barreau (mm) |
7.65 |
8 |
Hauteur du barreau (mm) |
47.5 |
100 |
Force maximum (N c. à c.) |
340 |
Supérieur à 1000 |
Déplacement max. (Ám c. à c.) |
55 |
120 |
Tableau -1 : Caractéristique des prototypes d'actionneurs à magnétostriction géante réalisés
Nous avons élaboré un premier prototype afin de nous familiariser avec la fabrication d'actionneurs magnétostrictifs et d'obtenir les premiers résultats validant les modélisations par éléments finis. Les caractéristiques techniques de cet actionneur sont décrites dans le Tableau IV-1. La taille du barreau est imposée. Nous avons donc conçu l'actionneur en fonction du barreau et des performances désirées. Nous choisissons volontairement un point de polarisation magnétique très bas pour réduire au maximum la taille de la bobine et la consommation électrique. Le champ statique est de 15 kA/m et le champ dynamique de 30 kA/m crête à crête. Les aimants, le circuit magnétique et la bobine sont donc dimensionnés en conséquence grâce à la modélisation. Avec de telles données, nous espérons atteindre un déplacement de 60 Ám (au vu des grandeurs magnétiques choisies et de la puissance électrique désirée). L'absence de certaines données nous empêche d'évaluer la force susceptible d'être développé par l'actionneur. A la suite des premières mesures, nous confirmons un déplacement de 60 Ám et nous avons obtenu les premières données concernant la force. Ce premier prototype a été conçu avec deux bobines. La seconde bobine, appelée " bobine intérieure " sur la Figure III-26, est utilisée pour faire varier le point de fonctionnement magnétique. Alimentée par un courant continu, elle nous a permis d'estimer l'influence de ce paramètre sur le fonctionnement global de l'actionneur.
Des modifications sur le premier prototype ont donné naissance au prototype N░2. La taille des aimants est augmentée (pour augmenter le champ statique), la bobine intérieure est retirée et la bobine qui permet de créer le champ dynamique a été sur-dimensionné. Nous avons ainsi augmenté la valeur globale des grandeurs magnétiques afin de pouvoir pousser plus loin les mesures de force.
Enfin, grâce aux connaissances acquises sur ces deux premiers prototypes, nous avons fabriqué les prototypes 3 et 4 qui sont identiques et conformes au cahier des charges. Ces deux derniers prototypes ont été utilisés dans la tâche 7 pour les applications industrielles du contrôle actif des vibrations et de tests de vieillissement de structure. Ces actionneurs ont alors subi des essais au-delà de leur seuil de tolérance pour que des mesures d'hystérésis et de température soient possibles.
Les grandeurs magnétiques sont des paramètres importants pour la compréhension du comportement des actionneurs magnétostrictifs. Il est donc nécessaire d'intégrer dès la conception de l'actionneur un système qui permettra de réaliser ces mesures magnétiques. Les grandeurs concernées sont : le champ, l'induction dans le barreau ainsi que sa perméabilité.
L'induction magnétique peut être mesurée à l'aide d'une sonde à effet Hall ou par des bobines de mesure. La première solution (capteur à effet Hall) oblige par son principe à placer la sonde au centre du barreau. Ce dernier se travaille difficilement (car très dur et cassant). Il nous a paru donc difficile de le percer pour y placer un capteur à l'intérieur. De plus le barreau subit des contraintes mécaniques importantes et il serait inconcevable de le fragiliser par un quelconque usinage. La deuxième solution (mesure de l'induction à l'aide de bobines) est la mieux adaptée à nos contraintes. Il est également possible par combinaison de deux bobines de mesurer le champ et d'en déduire la perméabilité du barreau magnétostrictif. Ces mesures donneront les valeurs moyennes des grandeurs magnétiques dans le barreau. Toutefois la distribution du champ radial au barreau ne peut pas se mesurer expérimentalement.
Ce système de mesures par bobine implique de travailler en régime dynamique. Cette condition n'implique aucun désavantage dans notre cas. La variation du flux à travers ces bobines induit alors une tension à leurs bornes suivant la loi :
![]()
e : tension induite aux bornes de la bobine
n : nombre de tours de la bobine
f : flux magnétique
Le principe de mesure est le suivant : deux bobines sont placées autour du barreau à l'endroit où la mesure doit être relevée, en l'occurrence au milieu du barreau. Voir Figure IV-1.
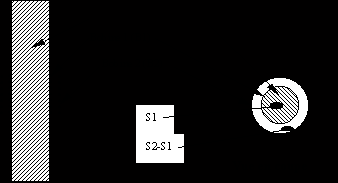
Figure -1 : Détails du système de mesure magnétique
Nous calculons l'induction magnétique à l'aide d'une seule bobine.
La bobine B1 enroulée sur le barreau permet de mesurer l'induction dans le barreau.
|
|
Eq. 41 |
D'où ![]() devient
devient
|
Eq. 42 |
Sachant que ![]() avec S section transversale de la bobine.
avec S section transversale de la bobine.
Et en supposant que le flux dans la bobine est perpendiculaire à la surface qu'elle entoure, nous obtenons comme expression pour l'induction dans le barreau :
![]()
![]() : surface entourée par la bobine B1
: surface entourée par la bobine B1
Soit :
|
Eq. 43 |
Pour calculer le champ magnétique, on sait d'après les hypothèses fixées :
![]() flux à travers la bobine B1
flux à travers la bobine B1
|
|
Eq. 44 |
Donc |
Eq. 45 |
De plus :
|
Eq. 46 |
En posant comme condition : ![]() :
:
|
Eq. 47 |
Nous avons alors en régime harmonique :
|
Eq. 48 |
Nous pouvons ainsi en déduire la perméabilité du barreau :
![]() ce qui donne,
ce qui donne,
|
Eq. 49 |
La précision des mesures dépendra principalement de la différence entre S1 et S2. Plus elle sera importante plus les mesures seront précises. Comme les bobines de mesures sont placées entre le barreau et le bobinage principal créant le champ, l'espace reste limité. La mesure doit être faite le plus près possible du barreau. car plus nous nous éloignons du barreau, plus H varie.
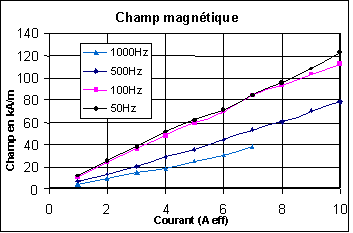
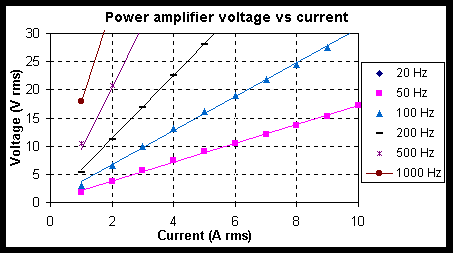
Figure -2: Champ magnétique en fonction du courant à 20 Mpa de pré-contrainte pour différentes fréquences
Sur la Figure IV-3, le champ magnétique diminue lorsque la fréquence augmente. Les courbes ne sont ici plus linéaires bien que nous soyions en dessous de la saturation magnétique du matériau magnétostrictif. En fait, cette non-linéarité est due à la réduction de la perméabilité magnétique du Terfenol-D en fonction du courant (cf. Figure IV-4).
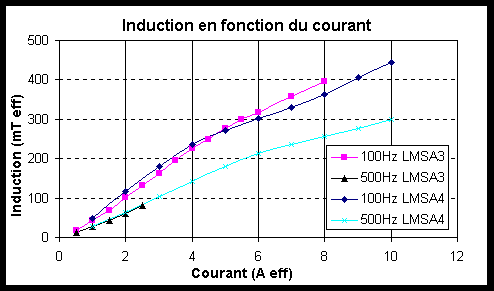
Sur la Figure IV-2, nous pouvons observer la décroissance de l'induction en fonction de la fréquence. Cette décroissance s'explique par les courants de Foucault qui augmentent lorsque la fréquence augmente principalement dans le barreau et un peu dans le circuit magnétique. En effet, le circuit magnétique est constitué de feuilles très fines de 0,1 mm d'épaisseur qui empêchent les courants de Foucault de se développer dans la bande de fréquence utilisée.
En dessous de 200 Hz, les courants de Foucault ont peu d'influence sur le champ magnétique. Par contre au-delà de cette fréquence les courants de Foucault, principalement développés dans le barreau magnétostrictif, réduisent le champ magnétique moyen jusqu'à un facteur 2,5 à 1000 Hz.
Nous pouvons constater aussi sur cette même figure que les courbes sont linéaires puisque le champ magnétique est proportionnel au courant.
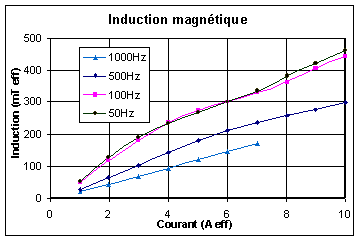
Figure -3: Induction en fonction du courant à différentes fréquences sous une précontrainte de 20 Mpa.
Les mesures de perméabilité magnétique du barreau présentées (cf. Figure IV-4) sont à admettre avec précaution. La précision des mesures dépend du rapport des surfaces des deux bobines de mesure (cf. paragraphe IV.2.1 ). En raison du faible espace libre autour du barreau (car la bobine d'alimentation est très près du barreau), ces bobines sont placées très proches l'une de l'autre donc une petite imperfection sur les dimensions d'une des bobines de mesure peut donner une erreur importante. Nous estimons donc que notre imprécision de mesure est d'au moins 20%. Toutefois, l'allure générale de la courbe reste vraie et les valeurs de perméabilité magnétique sont de l'ordre de celles citées dans la littérature.
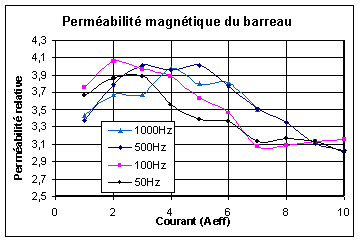
Figure -4: Perméabilité en fonction du courant à différentes fréquences pour une précontrainte de 20 Mpa.
La tendance est donc à la diminution de la perméabilité avec l'amplitude du courant.
Pour mesurer l'impact du champ statique sur le déplacement maximum, le premier prototype a été équipé d'une seconde bobine (cf. Figure III-26). Alimentée par un courant continu, elle permet de faire varier le champ statique.
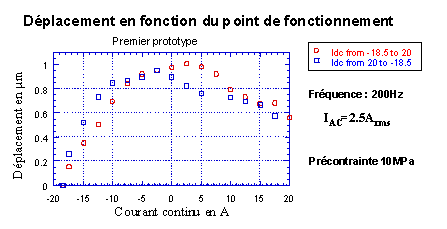
Figure -5 : Mesure de déplacement en fonction du champ statique sous faible champ dynamique.
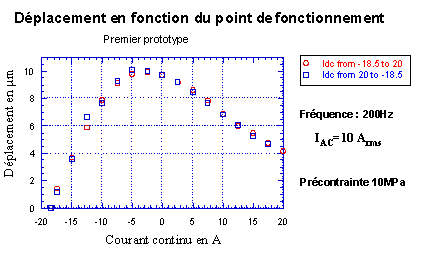
Figure -6: Mesure de déplacement en fonction du champ statique sous champ dynamique important.
Le déplacement maximal est obtenu pour un courant dans la bobine proche de zéro (cf. Figure IV-6). Ce résultat confirme le bon dimensionnement des aimants et valide les résultats obtenus à l'aide de la modélisation élément finis. Pour les prototypes suivants cette bobine a été retirée.
Nous constatons également que l'hystérésis a une influence relative plus importante lorsque le champ dynamique est faible (cf. Figure IV-5).
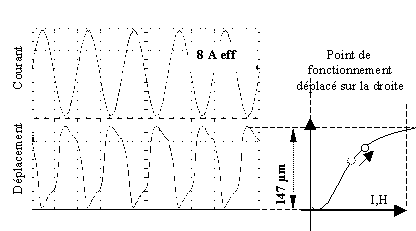
Figure -7 : Déplacement du point de fonctionnement vers la droite par ajout d'un courant continu de 3 A dans la bobine. Dans cette configuration nous obtenons le déplacement maximal de 147 Ám.
La Figure IV-7 et la Figure IV-8 représentent des mesures de déplacement effectuées sur le dernier prototype (LMSA4). Au courant sinusoïdal alimentant l'actionneur est superposé un courant continu dans le but de faire varier le point de fonctionnement. Pour obtenir le maximum de déplacement sans doublement de fréquence, le point de fonctionnement est décalé sur la droite (cf. Figure IV-7). Le courant continu ajouté dans la bobine est alors de 3 A. Nous obtenons ainsi un déplacement maximal de 147 Ám. A l'inverse, sur la Figure IV-8 le courant continu ajouté est négatif et le point de fonctionnement est déplacé vers la gauche. Il est placé ainsi dans une zone plus raide (où le coefficient d33 est élevé) et plus linéaire. Nous obtenons ainsi un déplacement important relatif en considération du courant alternatif injecté dans la bobine. Le déplacement se rapproche alors d'une sinusoïde.
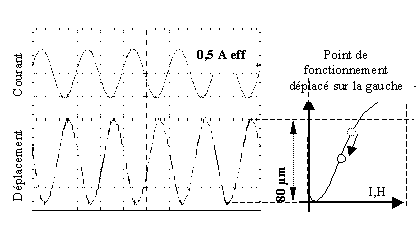
Figure -8 : Déplacement du point de fonctionnement vers la gauche par ajout d'un courant continu de -2,2 A dans la bobine. Dans cette configuration nous obtenons le maximum de déplacement pour un minimum de champ magnétique.
L'influence de la pré-contrainte est relativement complexe car elle dépend de l'amplitude du champ dynamique et du champ statique. La Figure IV-11 montre l'influence de la pré-contrainte sur le déplacement en fonction du champ magnétique. Pour des pré-contraintes faibles de 8 à 10 MPa, la valeur maximale de déplacement est rapidement atteinte sous faible champ.
La précontrainte a également comme nous le verrons dans le chapitre IV.3.3 une influence sur la force développée par l'actionneur
Nous utilisons deux méthodes différentes pour mesurer le déplacement. La mesure peut être faite directement à l'aide d'un capteur de déplacement (à courant de Foucault, interféromètre laser, etc.) ; dans les deux derniers prototypes un capteur de déplacement à courants de Foucault a été intégré pour faciliter la mesure. Nous pouvons également utiliser un accéléromètre positionné en sortie de l'actionneur, il suffira alors d'intégrer deux fois la mesure pour obtenir le déplacement. Dans les paragraphes IV.3.2.3 et IV.3.2.4 le déplacement est mesuré en sortie de l'actionneur avec un accéléromètre. Nous comparerons enfin les mesures obtenues avec le capteur interne présentée au paragraphe IV.3.2.5 .
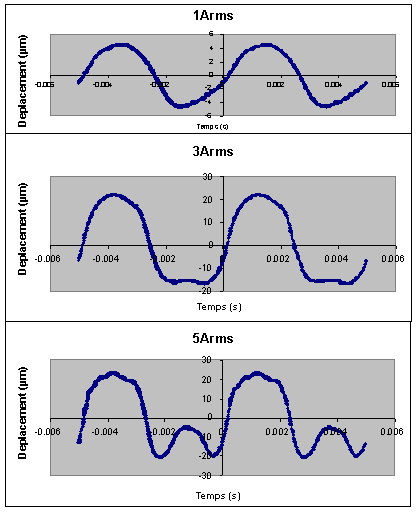
Figure -9 : Mesure de l'effet du doublement de fréquence (mesures effectuées sur le prototype N░1)
Le doublement de fréquence se produit lorsque le champ dynamique devient trop grand par rapport au champ statique. Sur la Figure IV-9, trois relevés temporels du déplacement illustrent l'effet du doublement de fréquence lorsque le champ dynamique devient trop important devant le champ statique. Nous éviterons ce phénomène en limitant la valeur maximale du courant d'alimentation.
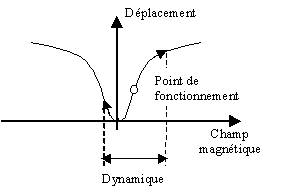
Figure -10: Explication du phénomène de doublement de fréquence.
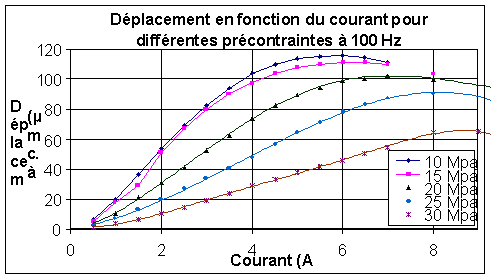
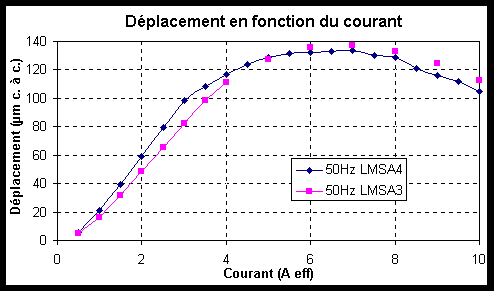
Figure -11: Déplacement en fonction du courant à différentes précontraintes pour une fréquence de 100Hz.
Le déplacement maximal obtenu est de 116 Ám crête à crête à 10 MPa de pré-contrainte. Cependant, nous ne choisirons pas une pré-contrainte de 10 MPa car le déplacement maximal n'est pas le seul critère. L'obtention de forces importantes, nous le verrons, impliquera d'utiliser une pré-contrainte supérieure. Ce compromis testé expérimentalement nous conduira aux alentours de 20 MPa. Comme une pré-contrainte de 20 MPa offre de meilleurs résultats en terme de force, nous retiendrons cette valeur. Il est également important de constater que le déplacement imposé par le cahier de charge de 100 Ám crête à crête est atteint avec cette pré-contrainte.
Nous pouvons constater que les courbes atteignent une valeur maximale puis redescendent entre 6 A et 8 A selon la valeur de la pré-contrainte. Ce phénomène est causé par l'augmentation de la distorsion harmonique. La non-linéarité devient si forte que certaines harmoniques deviennent importantes par rapport à la fréquence d'alimentation.
Les pertes par courants de Foucault et par hystérésis (pertes Fer) augmentent rapidement avec la fréquence[71,Sandlund] et le déplacement s'en trouve réduit. Elles réduisent le champ magnétique pénétrant dans le barreau et augmentent sa température en dissipant les courants induits par effet Joule. La température reste bien sûr inférieure à la température de Curie du matériau magnétostrictif mais elle croît suffisamment (cf. Paragraphe IV.4 ) pour dégrader les propriétés du matériau.
Les mesures de déplacement et de force sont limitées en fréquence par la puissance maximale de l'amplificateur utilisé.
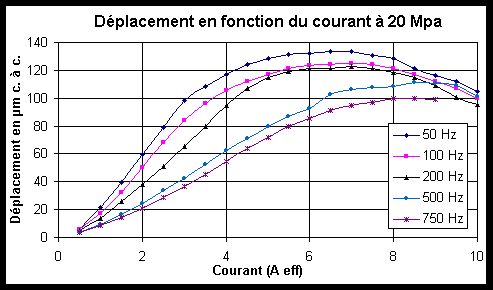
Figure -12: Déplacement en fonction du courant à différentes fréquences pour une précontrainte de 20 Mpa.
La Figure IV-13 montre la différence entre les résultats donnés par les deux méthodes de mesures présentées Paragraphe IV.3.2.1 . Sur cette figure, le " Capteur1 " représente la mesure faite avec le capteur de déplacement interne alors que le " Capteur2 " représente la mesure faite avec l'accéléromètre.
La différence entre les deux mesures est assez importante (environ 25%). Elle n'est pas causée par un problème de sensibilité ou de précision d'un des capteurs. La mesure la plus fiable correspond à celle de l'accéléromètre qui effectue une mesure directe en sortie de l'actionneur. En contrepartie pour des commodités de montage, le capteur de déplacement interne a été excentré du barreau et mesure le déplacement d'une plaque mise en mouvement indirectement par le barreau. Le léger flambage de cette plaque amplifie le mouvement de quelques micromètres et fausse la mesure.
Néanmoins, le capteur interne permet de s'affranchir d'une mesure extérieure pour certaines applications. Cette erreur de mesure n'a pas de conséquence pour réduire les vibrations d'une structure à l'endroit où l'actionneur sera mis en contact avec celle-ci. De plus, il est toujours possible de tenir compte de cet écart dans un système de contrôle.
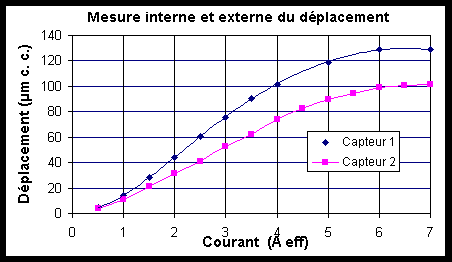
Figure -13: Comparaison entre le déplacement mesuré avec l'accéléromètre en sortie de l'actionneur et celui mesuré par le capteur de déplacement à courants de Foucault interne à l'actionneur. Mesures faites à 50Hz et 20 Mpa de précontrainte.
La distortion harmonique totale se calcule pour une certaine fréquence, ici la fréquence fondamentale. Seuls les multiples de cette fréquence sont pris en compte dans le calcul du THD. Le bruit qui peut exister entre le fondamental (Ao) et ses harmoniques (An) n'est pas pris en compte dans le THD. Le THD est calculé avec la formule ci-dessous :
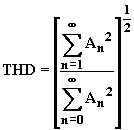
En pratique seuls les premières harmoniques mesurées sont utilisées car elles ont une amplitude significative devant le fondamental. Les autres sont considérés comme négligeables.
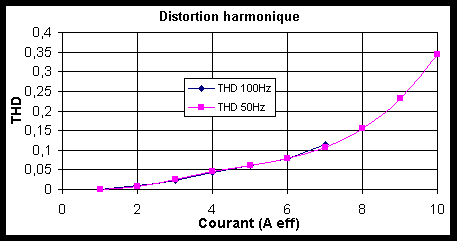
Figure -14: Distorsion harmonique du déplacement (THD, " Total Harmonic Distortion ") à 50 Hz et 100 Hz pour 20 Mpa de précontrainte.
La THD représente le taux de non-linéarité du signal analysé. La non-linéarité est relativement faible jusqu'à 6 Aeff. puis elle augmente. En effet au-delà de 6 A (courant positif), le déplacement commence à saturer. Alors que lorsque le courant passe en dessous de -6 A (courant négatif), le champ dynamique devient supérieur au champ statique créés par les aimants et augmente l'influence de l'harmonique deux (cf. paragraphe IV.3.2.2 ).
Le comportement dynamique des actionneurs magnétostrictifs est très différent des mesures statiques envisageables sur un barreau de Terfenol-D. Les Figures IV-15 montrent l'évolution du cycle d'hystérésis du déplacement en fonction du courant d'alimentation pour différentes fréquences. La première figure montre des mesures effectuées pour un parcourt de la boucle d'hystérésis à 0.5 Hz. Elles sont très proches des mesures statiques présentées Chapitre II . Mais on s'aperçoit que rapidement avec l'élévation de la fréquence le cycle d'hystérésis devient très large.
Ces mesures mettent en évidence les différences entre les comportements statiques et dynamiques. Ces différences ne sont pas une conséquence de la non-linéarité du phénomène magnétostrictif. Ces phénomènes complexes, qui se produisent en mode dynamique, existent également dans le cas d'un actionneur piézo-électrique (actionneur linéaire). Autrement dit, le terme linéarité n'a plus vraiment de sens en dynamique.
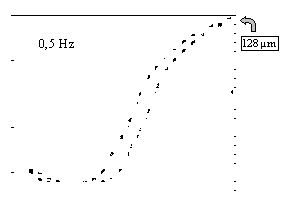
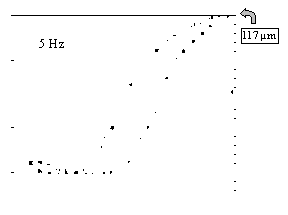
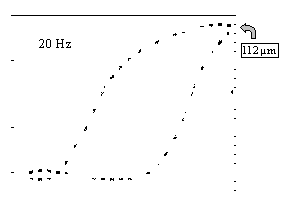
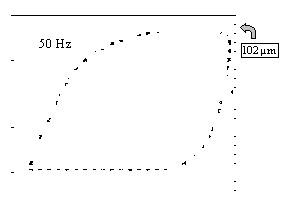
Figures -15 : Cycle d'hystétésis du déplacement en fonction du courant à différentes fréquences
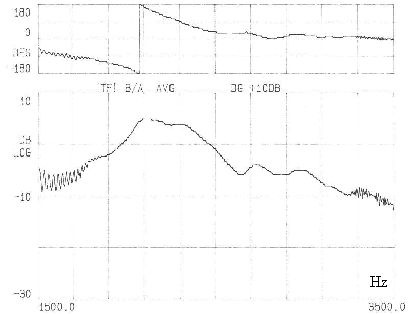
Figure -16 : Diagramme de Bode de l'accélération en fonction du courant d'alimentation. L'échelle en dB est arbitraire.
La Figure IV-16 représente la fonction de transfert en fonction de la fréquence du prototype N░4 de nos actionneurs magnétostrictifs. Elle montre les deux premières fréquences de résonance. La première se situe autour de 2100 Hz et la seconde est très proche. La mesure est effectuée sur l'actionneur libre, c'est à dire sans contrainte mécanique extérieure. Seule une précontrainte interne de 20 MPa est appliquée au barreau. Nous reverrons dans le Chapitre V que lorsqu'il est couplé à une masse, l'actionneur voit ses fréquences de résonance chuter (des explications théoriques sont données au chapitre II.4.2 ).
Pour mesurer la force, l'actionneur est placé à l'intérieur d'une structure qui a pour but d'empêcher tout déplacement de celui-ci. Cette structure est schématisée Figure IV-17. Par l'intermédiaire d'un capteur placé entre cette structure et la sortie de l'actionneur, la force développée par ce dernier peut être mesurée. Dans cette configuration l'actionneur peut exercer une force de traction et une force de compression sur le capteur.
La force de traction est développée par le système de précontrainte sur la structure lorsque le bobinage est alimenté par un courant négatif (la longueur du barreau est réduite). Lorsque le courant est positif le barreau s'allonge et il crée une force de compression sur la structure. La combinaison de ces forces de traction et de compression est mesurée par le capteur et détaillée ci-dessous.
L'intérêt de la force de traction dépend fortement de la configuration dans laquelle l'actionneur sera utilisé. S'il est utilisé comme support actif d'une structure, la précontrainte aura alors moins d'importance car le poids de cette structure servira de précontrainte mais aussi de masse de rappel donc plus besoin de traction. Elle risque même de pénaliser les performances de l'actionneur en créant une précontrainte trop importante. Par contre, si l'actionneur est utilisé comme une masse inertielle (configuration utilisée au Chapitre V pour le contrôle actif des vibrations) ou pour exciter une masse inertielle sur le plan horizontal alors le système de précontrainte a toute son importance. En effet dans ce cas là, les forces de traction et de compression seront réparties de façon égale. Il faudra donc choisir une précontrainte suffisamment importante pour permettre le rappel de la masse. Si celle-ci est trop faible il risquerait d'y avoir un décollement dans la chaîne de sortie (barreau + système de précontrainte) pouvant créer des chocs et par conséquent endommager l'actionneur.
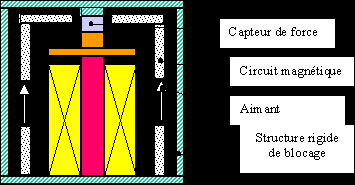
Figure -17: Représentation schématique de l'actionneur bloqué dans la structure, afin de mesurer la force développée.
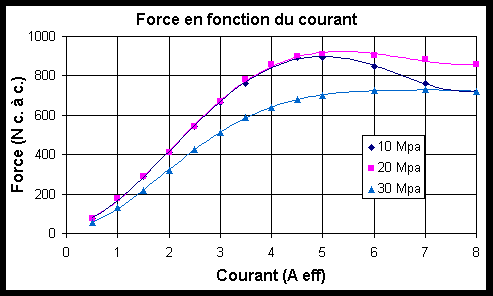
Figure -18: Force en fonction du courant pour différentes précontraintes à 100Hz.
La force maximale mesurée est de 905 N crête à crête à 20 Mpa de précontrainte (cf. Figure IV-18). Cette force reste inférieure à celle définie dans le cahier des charges. Certaines difficultés rencontrées nous amènent à penser que la force réelle pouvant être développée par l'actionneur est supérieure à celle mesurée. L'une des explications à cette observation est d'une part du à un problème technique détaillé au paragraphe IV.3.3.5 . D'autre part la structure n'est par parfaitement rigide et par exemple, nous mesurons à 905 N un déplacement de la structure de 6 Ám crête à crête. Ce léger déplacement réduit la force globale : le système n'est pas alors réellement bloqué et travaille en compression partielle.
La force développée diminue au-delà de 5 à 6 A et d'autant plus que la précontrainte est faible. C'est l'augmentation de la distorsion harmonique (THD) due à la non-linéarité des caractéristiques du barreau magnétostrictif qui en est la cause. De plus le système de précontrainte développe une force linéaire donc lorsque celle-ci augmente le taux de THD diminue. Voilà pourquoi la décroissance de la force est plus importante à faible précontrainte.
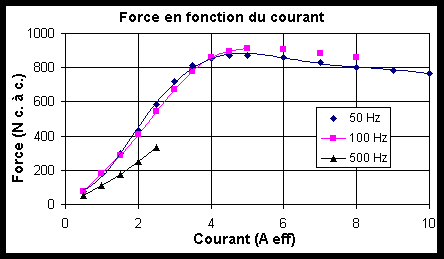
Figure -19: Force en fonction du courant à différentes fréquences pour une précontrainte de 20 Mpa.
La force est également affectée par la montée en fréquence. Les courants de Foucault ont, a priori, le même effet sur la force que sur le déplacement.
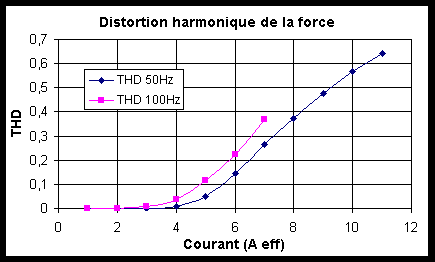
Figure -20: Taux de distorsion harmonique de la force pour un précontrainte de 20 Mpa.
Comme pour le déplacement, le taux de distorsion harmonique croît rapidement. Cette augmentation est liée au phénomène de doublement de fréquence et de saturation du déplacement.
Un problème technique tend également à réduire la force développée. La structure de blocage est réalisée en acier massif pour une rigidité maximale. Il en résulte que le matériau utilisé est ferromagnétique et sa perméabilité est élevée. L'actionneur est placé à l'intérieur de la structure et les aimants créant le champ statique se trouvent proches de celle-ci (cf. Figure IV-17). Une partie non négligeable du flux créé par les aimants se reboucle dans la structure et réduit d'autant le champ statique traversant le barreau. Par conséquent, le point de fonctionnement présenté Figure IV-10 se rapproche de zéro et le champ magnétique maximal atteint est diminué. Pour quantifier les pertes dues à cet effet, des mesures de déplacements ont été réalisées avec l'actionneur seul et l'actionneur dans la structure. Les résultats sont présentés sur la Figure IV-21. Le déplacement est réduit de 25% à 30% lorsque l'actionneur est placé à l'intérieur de la structure. Au vu de ce problème, nous pensons que la perte en force est également importante. Ainsi nous pensons que la valeur notifiée dans le cahier des charges est atteinte en condition réelle, soit 1000 N crête à crête.
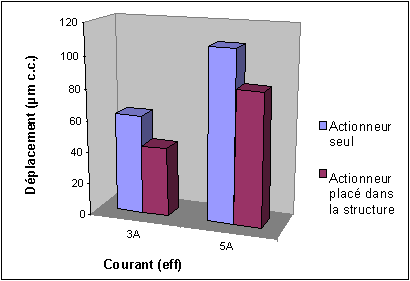
Figure -21: Influence de la structure sur le déplacement