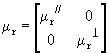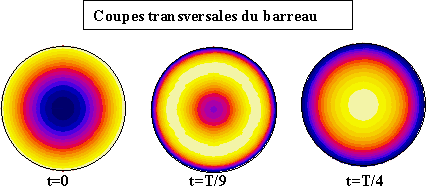• Dans un premier temps, nous étudions les différents composants et caractéristiques propres à un actionneur magnétostrictif. Ce sont les caractéristiques à évaluer lors de la conception des prototypes d'actionneurs à magnétostriction géante.
• La deuxième partie traite de la modélisation magnétique des actionneurs étudiés. Le LEG étant spécialisé dans ce domaine, des outils de conception sont développés depuis de nombreuses années au laboratoire. Ces logiciels de modélisation éléments finis appelés FLUX2D et FLUX3D sont commercialisés par la Société Cédrat (Meylan, Isère, France). Toutes les modélisations magnétiques présentées ci-dessous sont réalisées grâce à ces logiciels.
• Nous présentons ensuite, une modélisation thermique des actionneurs étudiés ainsi que les difficultés lors de cette analyse qui mériterait d'être approfondie.
• Nous terminons par les possibilités offertes, en terme de modélisation mécanique et magnéto-mécanique, par le logiciel éléments finis ATILA développé par l'Institut Supérieur d'Electronique du Nord.

1. Caractéristiques des différentes parties de l'actionneur magnétostrictif
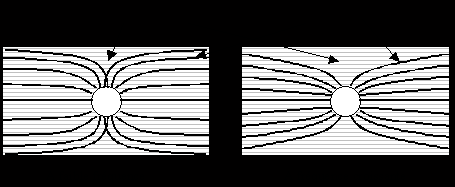
1. Structure

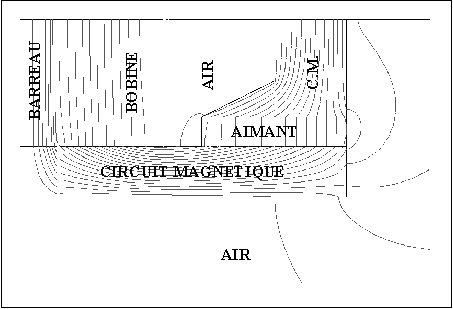
Deux conceptions très différentes peuvent être utilisées pour la réalisation de l'actionneur : soit une structure cylindrique (cf. Figure III-1) soit une structure plane (cf. Figure III-2). La structure circulaire semble, à priori, mieux adaptée puisqu'elle correspond à la forme naturelle du barreau. De plus, la comparaison des modélisations de ces deux structures (paragraphe III.3.2 ) a montré que la structure circulaire permettait d'atteindre des performances légèrement supérieures à la structure plane. Cependant un circuit magnétique de structure plane est beaucoup plus aisé à réaliser. Il suffit en effet de copier le circuit magnétique classique d'un transformateur. Cette structure a donc été choisie pour la réalisation de l'actionneur léger.



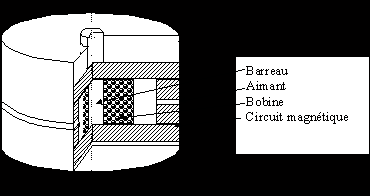
Figure -1 : Actionneur magnétostrictif de structure circulaire



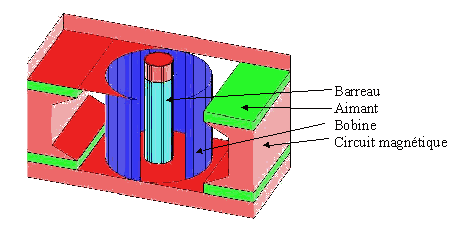
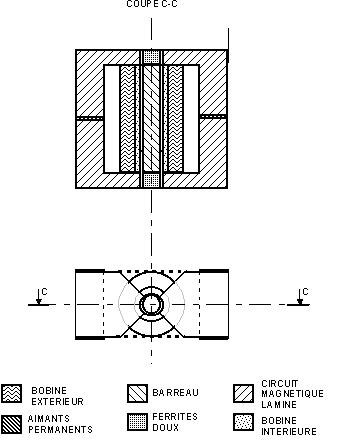
Figure -2 : Actionneur magnétostrictif de structure plane

Toutefois, notre partenaire allemand chargé de la réalisation de l'actionneur " lourd " a choisi une structure circulaire (Figure III-1). Les différentes pièces du circuit magnétique ont été réalisées en matériau magnétique laminé puis usinées pour permettre un assemblage circulaire. Les aimants ont également été " découpés " (usinage par électroérosion) pour pouvoir former une couronne autour du barreau. Les performances obtenues sont satisfaisantes malgré une géométrie complexe et difficile à réaliser. De plus, le circuit magnétique représentant la majorité du poids de l'actionneur, le poids est donc considérablement augmenté par rapport à une structure plane.

2. Le circuit magnétique

Le circuit magnétique peut être constitué de deux matériaux différents : alliage Fer-Silicium (ou Fe-Cobalt) laminé ou matériau ferrite doux Mn-Zn (fabriqué par la technologie des poudres). Les caractéristiques de ces matériaux sont présentées au chapitre II.2 .

Le fer doux laminé présente une grande perméabilité mais aussi une conductivité électrique importante. Comme l'actionneur magnétostrictif doit fonctionner à des fréquences relativement hautes (jusqu'à 1000 Hz), les feuilles de fer doux seront très fines (environ 0,1 mm d'épaisseur) pour limiter les pertes par courant induit dans le matériau. Cette technologie est fréquemment utilisée pour la plupart des circuits magnétiques (transformateur) et elle est particulièrement bien adaptée à la structure plane.

Certains matériaux magnétiques ferrites ont l'avantage d'avoir une faible conduction électrique, par conséquent, ils réduisent les courants induits (courant de Foucault). Ces matériaux possèdent également l'avantage de pouvoir être injectés et moulés comme les matériaux plastiques. Des formes complexes (cylindriques, sphériques) peuvent ainsi être obtenues. Néanmoins, une perméabilité et une induction magnétique à saturation relativement faible (voir paragraphe II.2.1 ) réduisent leurs performances. Ce type de matériau sera uniquement utilisé pour les éléments du circuit magnétique difficilement réalisables en Fer-Silicium Laminé, comme les pièces polaires (pièces cylindriques en dessus et en dessous du barreau magnétostrictif) car leur forme est cylindrique. De plus, le changement de direction du champ magnétique à cet endroit et enfin les efforts mécaniques supportés par ces pièces ne permettent pas de les réaliser en fer doux laminé.

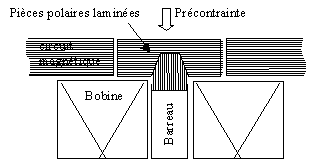
Un nouveau concept de pièces polaires en Fer-Silicium laminé a toutefois été proposé et modélisé par nos partenaires suédois^{[55,Stillesjo]}. Ils ont également déposé un brevet sur la conception de cette pièce. Ce concept consiste à usiner deux blocs de circuit laminé puis a les imbriquer perpendiculairement l'un de l'autre afin de permettre au champ un changement de direction de 90° comme présenté sur la Figure III-3. L'intérêt est de faciliter le changement de direction des lignes de champ. Un des actionneurs magnétostrictifs " lourd ", réalisé de cette façon, fonctionne correctement. Cette solution n'a pas été retenue pour l'actionneur léger car cette pièce est difficilement réalisable avec des feuilles très fines. De plus, la force développée par l'actionneur est transmise par l'intermédiaire de cette pièce polaire et la résistance mécanique de cet élément n'a pas encore été évalué lors d'une longue utilisation.



Figure -3 : Représentation d'une pièce polaire laminée

3. Les aimants

Les aimants créent le champ magnétique statique pour la pré-polarisation du barreau. Celui-ci peut facilement être obtenu avec des aimants de forme parallélépipédique dans le cas d'une structure plane. Ces aimants se comportent comme des entrefers à l'intérieur du circuit magnétique vis à vis du champ dynamique créé par la bobine. L'optimisation de la forme des aimants à l'aide des logiciels éléments finis nous conduit donc à l'élaboration d'aimants de larges dimensions et de faibles épaisseurs.

Des précautions doivent être prises lors de la manipulation des aimants dans l'air pour éviter leur démagnétisation lors du montage. Plus l'épaisseur de l'aimant est faible devant sa largeur et sa longueur, plus le champ démagnétisant est élevé en son milieu. A titre d'exemple ce phénomène est illustré sur la Figure III-4. Un aimant plat de 3 mm d'épaisseur, 10 mm de large et 20 mm de long entouré d'air est modélisé par le logiciel FLUX3D. Son champ rémanent est de 1 Tesla. Imaginons alors que cet aimant est constitué d'une multitude de petits aimants de hauteur 3 mm collés les uns contre les autres. Les lignes de champ créées par ces aimants doivent se refermer dans l'air. Celles créées par les aimants placés au centre parcourent un chemin bien plus grand que pour ceux situés sur les bords. Par conséquent, le champ démagnétisant au centre devient très important et dans ce cas il est égal à 650 kA/m.



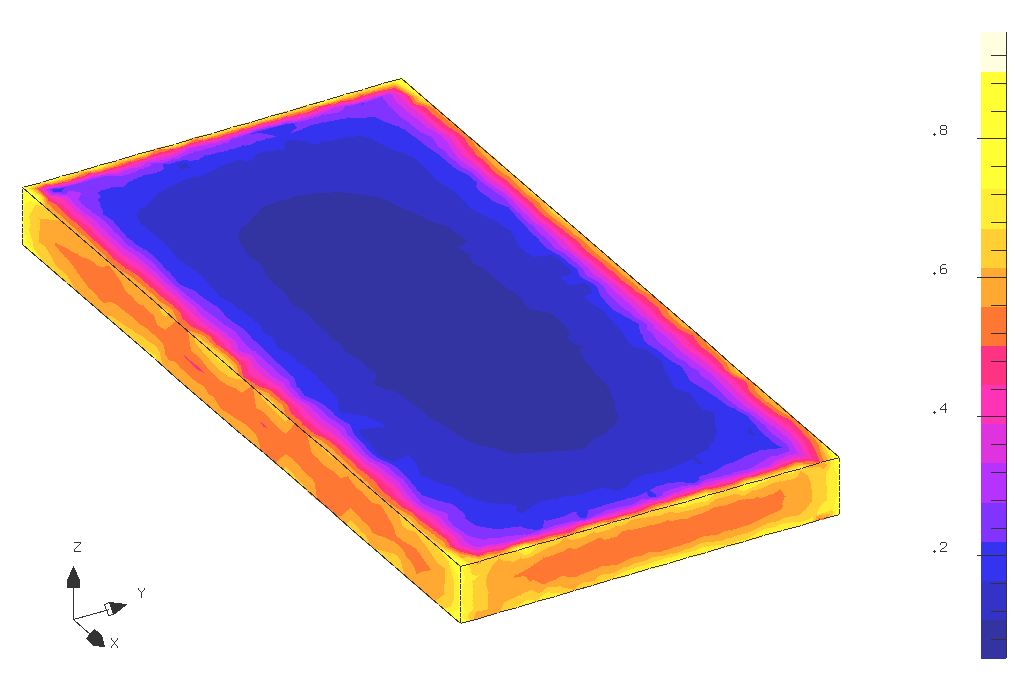
Figure -4: Modélisation de l'induction magnétique (Tesla) crée par un aimant plat dans l'air (champ rémanent de 1 Tesla). La polarisation est perpendiculaire au plan de l'aimant.

Si le champ démagnétisant devient trop important devant l'induction rémanente de l'aimant, ce dernier peut partiellement être désaimanté.

Actuellement les plus performants sur le marché, les aimants NdFeB semblent être les mieux adaptés pour la pré-polarisation du barreau. En effet les aimants NdFeB choisis ont une induction rémanente de 1.2 Tesla et un champ coercitif de 923 kA/m. Ils sont donc préservés de toute désaimantation dans l'air et dans l'actionneur magnétostrictif. Car il faut préciser que le champ créé par la bobine s'oppose pour les alternance négative du courant au champ statique des aimants et risquerait une fois de plus de les désaimanter. Ces aimants de très haute performance sont également très onéreux. Ce coût reste, toutefois, relativement faible comparé au prix du barreau magnétostrictif.

Nous pourrions envisager aussi un champ statique crée par un courant constant dans la bobine superposé au courant alternatif. Nous ne retiendrons pas cette solution pour trois raisons : le courant continu contribuerait à l'échauffement de la bobine et limiterait l'amplitude du courant alternatif, la consommation d'énergie serait plus importante, les amplificateurs audio qui pourrait être utilisés pour l'alimentation (ce sont des amplificateurs à faible coûts, tendance due à l'importance du marché) ne sont pas conçus pour délivrer un courant continu.

4. Le système de précontrainte

Pour des raisons d'encombrement, un système de précontrainte utilisant des rondelles " belleville " (rondelles coniques) est préféré au système classique de précontrainte par ressort. Cette solution permet également d'avoir des précontraintes élevées tout en travaillant bien en dessous des limites imposées par les rondelles " belleville ". Le déplacement imposé par le barreau au système de précontraintes étant très faible (100 µm maximum), la déformation en fonction de la force reste dans la zone linéaire imposée par les rondelles " belleville " et la précontrainte reste quasiment constante.

L'avantage majeur de ce système de précontrainte est sa compacité. Il permettra de réduire les dimensions extérieures de l'actionneur magnétostrictif.

5. Le bobinage

La bobine qui entoure le barreau peut être utilisée pour le champ dynamique et statique (pré-polarisation). Pour réduire la consommation électrique et les pertes thermiques qu'engendrerait un courant statique dans la bobine, le champ statique sera créé par des aimants. Il nous semble néanmoins intéressant de pouvoir ajuster ce champ statique. Deux solutions sont envisageables. La première, la plus simple, consisterait à superposer un courant continu au courant dynamique de commande. Cependant les amplificateurs utilisés lors des essais pour l'alimentation, ne délivraient pas de courant continu. La seconde solution nécessite un deuxième bobinage pour le réglage du champ statique. Celui-ci serait alimenté en courant pour s'affranchir des fluctuations de tension induites par le champ dynamique crée par la première bobine. Nous opterons pour cette dernière solution lors la construction du premier prototype d'actionneur léger afin de pouvoir faire varier le champ statique et de l'optimiser pour connaître son influence globale sur les performances de l'actionneur.

Le champ magnétique créé est proportionnel au courant d'alimentation de la bobine tandis que l'induction magnétique dépend des caractéristiques magnétiques du matériau (perméabilité, saturation, hystérésis).

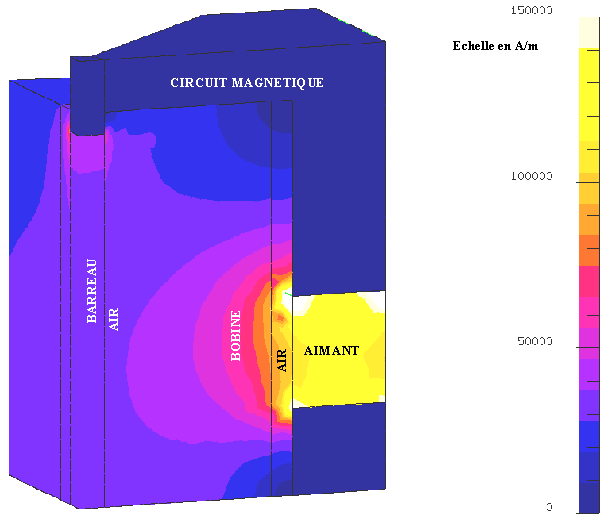
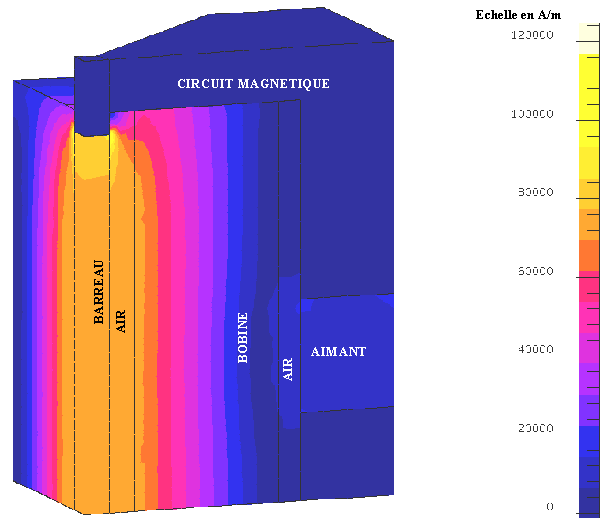
La valeur de l'inductance du bobinage dépend du nombre de tours mais également de la réluctance du circuit magnétique. Or le circuit magnétique est de forme complexe et il y a beaucoup de fuites du flux magnétique dans l'air dues aux matériaux à faible perméabilité comme les aimants et le barreau magnétostrictif. Il serait donc laborieux et très difficile de les estimer par un calcul analytique. Pour résoudre ce problème nous avons utilisé le logiciel de modélisation éléments finis FLUX3D dans lequel nous avons introduit la géométrie de l'actionneur avec ses différents matériaux et leurs propriétés magnétiques.

6. Le barreau magnétostrictif

Afin d'obtenir la plus grande déformation possible, nous avons choisi un barreau de type FSZM. Comme nous l'avons vu dans le chapitre II.1.6 , ce type de barreau est limité à un diamètre de l'ordre de 8 mm.

D'après les dernières caractéristiques des récents matériaux à magnétostriction géante mesurées par nos partenaires anglais de l'Université de Hull et de Salford, la déformation maximum obtenue est d'environ 2000 ppm (partie par million) sous un champ de 400 kA/m (précontrainte 20 MPa). Cependant 400 kA/m représente un champ très élevé non réalisable avec une puissance électrique raisonnable. Pour des raisons de consommation électrique, nous avons opté (pour les prototypes 3 et 4) pour un champ maximum autour de 120 kA/m. Un champ maximum plus faible ne permettrait pas, avec un barreau de 8 mm de diamètre, d'obtenir les forces désirées. Pour un champ maximum de 120 kA/m, la déformation obtenue étant plus faible (1650 ppm sous une précontrainte de 20 MPa), il convient de choisir un barreau plus long. Ainsi pour remplir le cahier des charges en terme de déplacement (100 µm), un barreau de 60 mm de long devrait théoriquement convenir. En pratique dans le cas d'un fonctionnement dynamique, les performances seront réduites. De plus, il est difficile d'obtenir un champ totalement homogène sur toute la longueur du barreau. Pour compenser ces problèmes, les barreaux utilisés pour les derniers prototypes ont une longueur plus importante de 100 mm. Nous verrons au Chapitre IV que les déplacements expérimentalement obtenus sont de l'ordre de 120 µm.

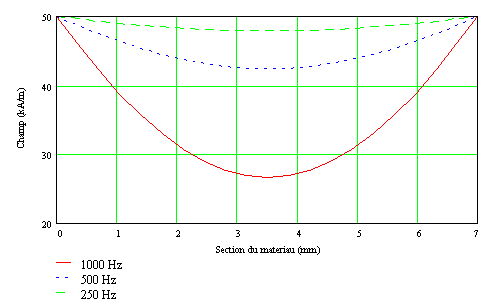
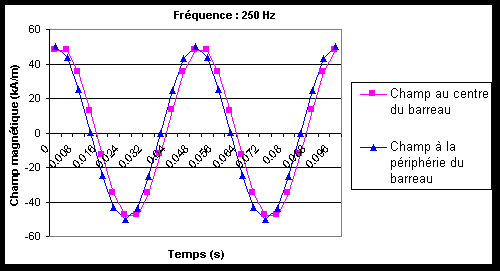
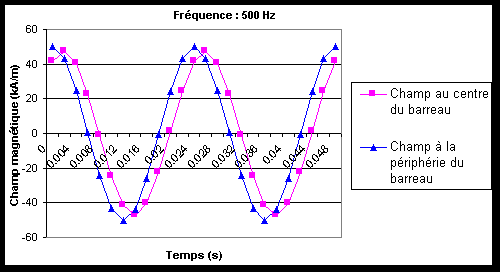
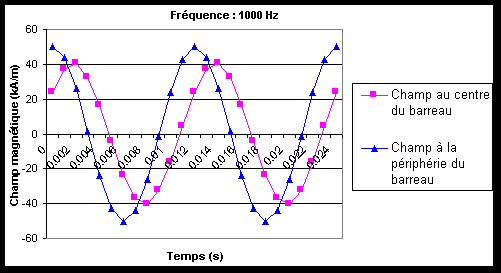
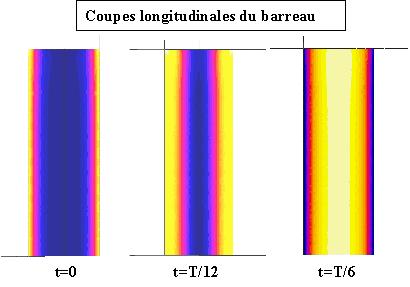
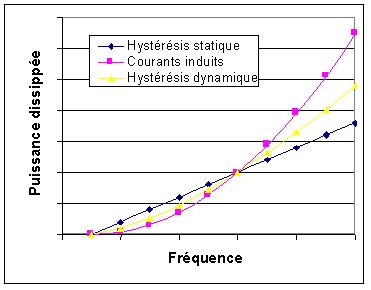
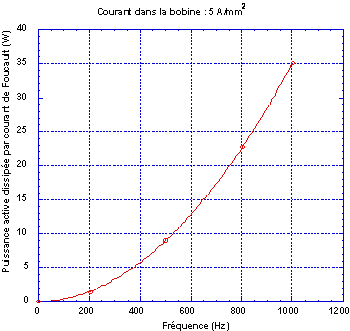
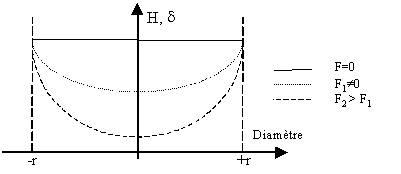
La faible perméabilité du Terfenol-D tend à réduire les courant induits alors que sa conductivité électrique très élevée, proche de celle du Fer, tend à l'augmenter. Des courants induits importants pourraient se développer dans le barreau au-dessus de 500 Hz. Ils dépendent de sa taille, de la précontrainte, de l'amplitude du courant et de la fréquence. La solution consisterait à laminer le barreau en plusieurs tranches^{[56,Stillesjö]}. Quatre tranches devraient suffire pour fonctionner jusqu'à 1000 Hz avec peu de pertes. Cependant le Terfenol-D est un matériau très cassant, il est donc difficile à usiner. Les techniques d'usinage classiques ne peuvent donc être utilisées. Il est possible de découper le barreau par électro-érosion mais l'opération devient longue et coûteuse. De plus, cette astuce ne fait pas partie du cahier des charges. Il serait toutefois intéressant de réaliser ultérieurement cette expérience pour en connaître l'intérêt exact.

7. Capteurs

• Capteurs magnétiques : de petits bobinages disposés autour et à proximité du barreau (détail au paragraphe IV.2.1 ) permettent les mesures du champ et de l'induction, et par conséquent la mesure de la perméabilité magnétique du barreau magnétostrictif.
• Capteurs thermiques : le capteur ne doit pas être sensible au champ magnétique, il est collé sur le milieu du barreau entre ce dernier et la bobine. Il permettra de connaître la température au cœur du système. Cette température croît à cause des pertes joules dans la bobine d'alimentation et par les courants induits développés dans le barreau.
• Capteurs mécaniques : deux types de capteurs seront utilisés. Un capteur de force permettra de mesurer la force maximale développée par l'actionneur et un capteur de déplacement nous donnera accès aux grandeurs mécaniques suivantes : déplacement, vitesse et accélération.

1. La modélisation magnétique
1. Introduction

• perméabilité relative du Fer-Silicium
• perméabilité relative de l'isolant
• épaisseur d'une feuille de Fer-Silicium
• 

1. Comparaison entre structure circulaire et structure plane

Des modélisations éléments finis ont été réalisées sur ces deux structures afin de déterminer le gain de performance de la structure circulaire sur la structure plane.

Les lignes de champ dynamiques créées par la bobine et traversant le barreau sont peu modifiées dans les deux cas. Le choix de la structure a donc peu d'importance pour le champ dynamique.

Par contre les lignes de champ statiques créées par les aimants à l'extérieur du barreau sont guidées jusqu'à celui-ci par le circuit magnétique. Sa géométrie intervient donc en facilitant plus ou moins l'arrivée des lignes de champ sur le barreau. Pour comparer de façon correcte les deux structures, la même quantité d'aimant a été utilisée dans les deux cas. La modélisation éléments finis montre que la structure circulaire dans ce cas présente un rendement supérieur de 15% par rapport à la structure plane. Nous entendons par rendement le rapport de la quantité de flux magnétique qui traverse effectivement le barreau sur la quantité de flux magnétique totale créée par les aimants.

Le principal inconvénient de la structure circulaire est sa complexité de réalisation. Elle nécessite l'usinage du circuit magnétique laminé pour permettre l'assemblage sous forme circulaire. Plus les feuilles sont fines, plus l'usinage devient délicat. Les aimants doivent être découpés par électroérosion pour former une couronne autour du barreau.

En raison de la difficulté d'usiner le circuit magnétique des prototypes d'actionneurs " légers " (car les feuilles Fer-Silicium utilisées pour la réalisation du circuit magnétique sont de très faible épaisseur) et malgré un rendement légèrement inférieur, nous avons choisi de réaliser ces prototypes avec une structure plane.

2. Caractéristiques de la bobine

La bobine a été dimensionnée pour obtenir le champ magnétique maximal désiré avec une densité de courant de l'ordre de 2 à 3 A/mm2. Un champ plus important pourra toutefois être obtenu en augmentant la densité de courant jusqu'à 5 A/mm2. Elle a un nombre de tours identique sur toute sa longueur, mais il est également possible de travailler sur une répartition irrégulière des spires pour essayer d'agir sur l'homogénéité du champ dans le barreau^[6,Qiang]. La bobine interne permet d'ajuster le champ statique créé par les aimants et la bobine externe crée le champ dynamique (prototype N°1).

3. Les lignes de champ dans le circuit magnétique

Les résultats des modélisations ont montré qu'environ la moitié du champ créé par la bobine traverse le barreau alors que seulement quelques pour-cent du champ créé par les aimants le traverse. Ces résultats sont principalement dus à la faible perméabilité du barreau magnétostrictif (entre 4 et 20 suivant les conditions d'utilisation) et sont illustrés sur les Figure III-9 et Figure III-10.



Figure -9 : Champ magnétique créé par les aimants, champ statique.



Figure -10: Champ magnétique créé par la bobine, champ dynamique.

La totalité du flux magnétique est représentée par une largeur de 20 lignes de champ côte à côte, c'est à dire qu'il circule environ 5% du flux entre deux lignes. Nous nous apercevons donc que seulement quelques pour-cent (2% or 3%) du flux créé par les aimants passent dans le barreau (le flux perdu ou flux de fuite représente alors 97 % à 98 % du flux total créé par les aimants). Les aimants seront donc de taille importante. La Figure III-10 montre que dans le cas des lignes de champ créées par la bobine environ 50% du flux traverse le barreau.

4. Distribution du champ magnétique dans le barreau

Les dégradés de couleurs de la Figure III-11 et de la Figure III-12 représentent la distribution du champ magnétique créée respectivement par les aimants et la bobine. Seul 1/8^ième de l'actionneur est représenté car sa structure plane comporte trois plans de symétries.

De nombreuses modélisations ont été réalisées pour différentes tailles d'aimants, et de bobines. Nous faisons alors varier la géométrie des différentes pièces pour obtenir la valeur de champ désirée répartie de façon la plus homogène possible dans le barreau. Une répartition hétérogène du champ magnétique conduirait à augmenter la non-linéarité de l'actionneur.



Figure -11 : La distribution du champ magnétique en A/m créée par les aimants et calculée avec le logiciel FLUX3D.



Figure -12 : La distribution du champ magnétique en A/m créée par la bobine et calculée avec le logiciel FLUX3D.

Sur la Figure III-11, nous voyons que la répartition du champ statique dépend beaucoup de l'emplacement des aimants. Plus il y aura d'aimants repartis sur toute la longueur du barreau, plus le champ statique sera homogène.

Le champ dynamique créé par la bobine (cf. Figure III-12) est beaucoup plus homogène car la densité de courant créant ce champ est uniformément répartie tout le long du barreau.

Sur les deux figures, nous constatons que le champ est plus important aux extrémités du barreau qu'au milieu (la partie basse n'est pas représentée sur les figures à cause des symétries). Le circuit magnétique de perméabilité très élevée concentre les lignes de champ dans le barreau. Une partie de ces lignes de champ vont sortir du barreau, car sa perméabilité relative est très faible (environ 5) pour se répartir dans l'air qui l'entoure.

5. Effet de la fréquence sur la distribution du champ magnétique dans le barreau

Les résultats suivants sont issus des modélisations par éléments finis effectuées sur FLUX3D. L'actionneur est alimenté par un courant sinusoïdal. Le but de ces modélisations est de mettre en évidence, les phénomènes dus aux courants induits développés dans le barreau. Elles ne prennent pas en compte les phénomènes d'hystérésis et de saturation. Mais ce dernier phénomène n'a qu'une importance relative dans notre cas, car les valeurs de champ sont en dessous des valeurs de saturation magnétique du matériau.

L'évolution dans le temps du champ magnétique sur l'axe du barreau et à la périphérie pour trois fréquences différentes est représentée Figure III-14. Nous constatons que la valeur efficace du champ au centre de barreau diminue quand la fréquence augmente. Le second phénomène intéressant est le déphasage qui apparaît entre le champ au centre et le champ à la périphérie du barreau.

La Figure III-13 montre clairement à l'instant t=0, (instant où le champ est maximal en périphérie du barreau) la variation du champ suivant le diamètre du barreau. A 250 Hz, le champ au centre est 4% plus faible qu'à la périphérie. Cette réduction est de 14 % à 500  Hz et de 46 % à 1000 Hz.



Figure -13 : Evolution à t = 0 du champ magnétique le long du diamètre du barreau pour trois fréquences différentes : 250 Hz, 500 Hz, 1000 Hz. Perméabilité relative 5, conductivité 1,66.10⁶ W .m, diamètre 7 mm.







Figure -14 : Evolution dans le temps du champ magnétique sur l'axe et à la périphérie du barreau pour trois fréquences différentes : 250 Hz, 500 Hz, 1000 Hz. Perméabilité relative 5, conductivité 1,66.10⁶ W .m, diamètre 7 mm.

 

Par moment, le champ est plus important en périphérie, alors qu'à d'autres instants, il est plus important au centre. Ce phénomène est illustré sur la Figure III-15 et la Figure III-16. Les couleurs claires représentent les endroits où le champ est le plus important.



Figure -15 : Illustration de l'évolution du champ dans le barreau à trois instants différents : t=0, t=T/12, t=T/6. Plus la couleur est claire plus le champ est important. Coupes longitudinales du barreau



Figure -16 : Illustration de l'évolution du champ dans le barreau à trois instants différents : t=0, t=T/9, t=T/4. Plus la couleur est claire plus le champ est important. Coupes transversales du barreau.

Nous pouvons en déduire que ces variations radiales du champ magnétique créent des contraintes mécaniques à l'intérieur du matériau. Ces contraintes réduisent évidemment les déplacements attendus lorsque la fréquence augmente. Par conséquent, la déformation en bout du barreau n'est pas homogène et les efforts qu'il supporte ne sont plus repartis sur toute la surface mais dépendent de la forme de celle-ci. Aucune mesure n'a pu être réalisée pour mettre en évidence les déformations réelles de la surface du barreau. Par contre, nous avons pu constater qu'à fréquence élevée, les bords de cette surface se sont rompus sur les différents actionneurs. Nous supposons que lorsque le champ devient grand en périphérie par rapport au centre, l'allongement du barreau est plus important en périphérie et les surfaces en bouts de barreau prennent la forme d'une cuvette. A cet instant, toute la contrainte appliquée au barreau est seulement répartie sur les bords de ces surfaces qui cèdent sous la pression.

6. Alimentation électrique

1. La modélisation thermique

La modélisation thermique ne représente pas le principal de notre travail de modélisation. Elle n'était, en particulier, même pas prévue dans le contrat initial. Cependant à la demande des partenaires quelques calculs élémentaires ont été menés Un calcul sérieux et rigoureux nécessiterait un investissement de temps plus important pour évaluer précisément les différents phénomènes thermiques mis en présence. De plus l'absence de données concernant les pertes magnétiques des matériaux magnétostrictifs ne nous permet pas pour l'instant de chiffrer l'influence de chaque effet. Il faudrait pour cela entreprendre une série de mesures thermiques et magnétiques et nous sortirions du cadre de cette thèse. Nous reconnaissons cependant l'intérêt de connaître les sources de chaleur responsables de l'élévation de température d'un actionneur magnétostrictif.

Plusieurs phénomènes physiques dégagent de la chaleur au sein de l'actionneur. Il est important de les connaître afin de quantifier ces sources de chaleur. Nous pourrons ainsi déterminer les limites de fonctionnement imposées par cette élévation de température.

Nous avons identifié cinq sources : les pertes par hystérésis à basse fréquences que nous appellerons " pertes par hystérésis statique ", les pertes par hystérésis dues à l'élargissement du cycle lorsque la fréquence augmente que nous appellerons " pertes par hystérésis dynamique ", les pertes Joule par courants induits, les pertes Joule dans la bobine et les pertes purement mécaniques. Les trois premières se produisent dans le barreau magnétostrictif et le circuit magnétique laminé. Nous n'avons trouvé aucune donnée précise concernant les pertes purement mécaniques dues aux efforts exercés sur le barreau,. Pour cette raison, ces pertes que nous supposerons à priori faibles devant les autres sources de perte de chaleur ne seront pas prises en compte.

1. Pertes dans le barreau magnétostrictif

La Figure III-17 illustre l'évolution de la puissance perdue dans le barreau par des phénomènes d'hystérésis statiques et dynamiques et par pertes Joule dues aux courants induits dans le barreau. Pour simplement illustrer ces différents phénomènes dans cette figure nous avons choisi des échelles arbitraires.



Figure -17 : Illustration des pertes par hystérésis statiques, hystérésis dynamiques et par courants induits dans le barreau magnétostrictif.

 

1. Pertes par hystérésis statiques et dynamiques

Les pertes par hystérésis statiques et dynamiques sont estimées en calculant l'aire décrite sous la courbe du cycle d'hystérésis de la courbe B(H). L'énergie perdue par cycle est :

Eq. 39

Egalement appelées " pertes Fer ", ces pertes sont dues aux frottements des moments magnétiques les uns contre les autres lorsque les lignes de champs changent de direction. Ils sont la cause de l'hystérésis du matériau et ce surplus d'énergie nécessaire à la rotation des moments magnétiques est dissipé sous forme de chaleur.

Les pertes dites par " hystérésis statiques " correspondent à l'aire décrite par le cycle B(H) et mesurées de façon quasi-statique. Ces pertes sont proportionnelles au nombre de cycles parcourus et par conséquent elles sont proportionnelles à la fréquence ().

Les pertes dites par " hystérésis dynamique " représentent l'élargissement du cycle d'hystérésis lorsque la fréquence augmente en l'absence de courants induits. Elles suivent la loi : où F est la fréquence.

 

2. Pertes Joule dues aux courants induits dans le barreau.

Fréquence (Hz)	100	500	1000	1500	2000
Epaisseur de peau pour µr=5 (mm)	17,4	7,8	5,5	4,5	3,9
Epaisseur de peau pour µr=20 (mm)	8,7	3,9	2,76	2,25	1,95

• µ : perméabilité
• µ = µo.µr µr : perméabilité relative du matériau, µ₀ : perméabilité dans le vide
• s (W .m) : conductivité électrique
• f (Hz) : fréquence en Hz

1. Pertes par effet Joule dues au courant d'alimentation dans la bobine

La première source de chaleur à forte densité de courant est l'énergie dissipée par effet Joule dans la bobine. La puissance dissipée dans cet élément s'exprime en fonction du carré du courant qui le traverse multiplié par la résistance de la bobine. La Figure III-21, issue du stage de DEA de Frédéric LEPOITEVIN, représente la distribution de la température dans la bobine et dans le barreau créée par effet joule. Ces pertes sont causées par le courant d'alimentation dans la bobine.



Figure -21 : Répartition de la température dissipée par effet Joule dans la bobine

Pour calculer précisément la dissipation thermique dans la bobine, il convient de connaître sa conductivité thermique. Or, pour maintenir fermement les spires de la bobine, nous utilisons une colle. Il est donc difficile de prendre en compte dans notre modélisation les dissipations réelles dans les spires de la bobine. De plus, la bobine est enfermée dans le boîtier et il devient difficile d'apprécier les différents échanges thermiques par convection et par rayonnement vers l'extérieur de celui-ci. Ces échanges thermiques dépendent notamment des conditions de ventilation et de la température extérieure. Pour ces raisons, les résultats numériques de la Figure III-21 ne sont pas pertinents.

Notons que ces pertes là, ne dépendent pas de la fréquence.

2. Conclusion

1. La modélisation mécanique

Pour la modélisation mécanique, nous travaillerons sur le logiciel " ATILA " (commercialisé par la Cédrat, Meylan, Isère, France). Ce logiciel éléments finis permet de modéliser des phénomènes physiques magnéto-mécaniques et électromécaniques. Il calcule les modes propres d'une structure (cf. Figure III-22), les fréquences de résonance et d'anti-résonance d'un mode couplé, et il permet d'effectuer une analyse harmonique.



Figure -22 : Quatrième mode propre longitudinal d'un barreau magnétostrictif

Adapté aux problèmes couplés linéaires, il convient particulièrement à la modélisation des phénomènes piézo-magnétiques et piézo-électriques. Toutefois dans le cas de couplages fortement non-linéaires comme c'est le cas pour la magnétostriction géante, l'intérêt est plus réduit. En effet, des modélisations concernant la force développée par l'actionneur ne se sont pas avérées satisfaisantes.

Notre partenaire Suédois a donc réalisé la plupart des modélisations magnéto-mécaniques à l'aide d'un logiciel approprié développé dans leur laboratoire. Nous nous sommes donc peu impliqués dans ce domaine. Leurs outils de modélisation permettent de tenir compte tant du couplage magnéto-mécanique, du circuit électrique et du circuit magnétique que de la contrainte appliquée à l'actionneur.



Figure -23 : Description du modèle développé par le KTH pour la modélisation des actionneurs.

La Figure III-23 présente le modèle développé par le KTH pour la modélisation des actionneurs. L'outil est basé sur la description du barreau de Terfenol-D par une approximation des différences finies utilisant la loi de Newton. Le barreau est divisé en n éléments axiaux et m éléments radiaux. Différentes grandeurs physiques peuvent être calculées dans le temps, comme le champ magnétique, l'induction magnétique, la force et le déplacement. Le couplage, avec les équations de circuit électrique (cf. Figure III-24) permet également d'avoir accès aux grandeurs électriques. Un résultat de simulation de force et de déplacement développés par l'actionneur alimenté par une sinusoïde est représenté sur la Figure III-25. L'effet de doublement de fréquence est mis en évidence (courbe de déplacement). Il est dû à la non-linéarité des matériaux magnétostrictifs. L'écrasement des crêtes positives de la courbe de déplacement montre la prise en compte du phénomène de saturation. La non-symétrie de ces crêtes est causé par le phénomène d'hystérésis.



Figure -24 : Circuit équivalent pour l'étude d'un actionneur magnétostrictif.. M_act et k_act sont respectivement la masse inertielle et la rigidité.



Figure -25 : Simulation de force et de déplacement réalisée par le KTH Royal Institute of Technology (Suède)

Toutefois, il faudrait une connaissance plus approfondie de leur outil de modélisation pour pouvoir estimer ses performances réelles.

2. Exemple de choix de conception du prototype d'actionneur " léger "

• La structure est plane pour en faciliter la réalisation
• Le circuit magnétique est en fer doux (Fe Si) laminé et les deux pièces polaires sont en matériaux doux frittés.
• Le système de précontrainte est réalisé à l'aide de rondelles " belleville " (rondelles coniques) ajustables de 10 MPa à 30 MPa. Les rondelles " bellevilles " permettent de réduire l'encombrement et elles rajoutent très peu d'inertie au système
• Les caractéristiques magnétiques sont :

• 60 kA/m pour le champ statique créé par les aimants
• ± 120 kA/m crête à crête pour le champ dynamique créé par la bobine

• Dans cette gamme de champ magnétique le déplacement maximal pouvant être obtenu est de l'ordre de 1200 à 1500 ppm (partie par million). Ainsi un barreau de 100 mm de long devrait nous permettre de dépasser le déplacement de 100 µm crête à crête défini dans le cahier des charges. Un diamètre de 8 mm devrait permettre de développer une force de 1000 N crête à crête.
• Le barreau n'étant pas laminé, les courants induits deviennent importants qu'au-delà de 500 Hz.

1. Conclusion