- Rétrospectives
- L'effet magnétostrictif
- Les matériaux magnétostrictifs
- Introduction
- Les terres rares
- Les principaux effets magnétostrictifs
- Un peu de théorie
Il existe deux effets magnétostrictifs, l'un appelé effet magnétostrictif spontané et l'autre (qui nous intéresse plus particulièrement et que l'on étudiera par la suite) appelé magnétostriction de Joule. L'effet magnétostrictif spontané se caractérise par une variation permanente en volume du matériau par rapport à celui qu'il occuperait s'il n'était pas magnétique. L'effet magnétostrictif de Joule, découvert en 1842 par James Prescott Joule, consiste en une déformation à volume constant du matériau lorsqu'il est soumis à un champ magnétique extérieur.
Au terme magnétostriction est associé depuis longtemps un des inconvénients majeurs de l'appareillage électrique : les bruits et vibrations à fréquences fixes engendrés par ces appareils. La nuisance acoustique et vibratoire due aux déformations mécaniques provoquées par la magnétostriction des matériaux ferromagnétiques est donc l'une des principales conséquences de la magnétostriction. Cette nuisance se retrouve dans de nombreuses machines électriques comme les transformateurs et les machines tournantes.
Cependant la magnétostriction est aussi un phénomène utilisé avec profit. Les militaires furent les premiers à utiliser des matériaux magnétostrictifs pendant la seconde guerre mondiale pour les sonars des sous-marins. Les deux principaux avantages de ces matériaux sont d'une part de pouvoir émettre (mode transducteur) et recevoir des ondes acoustiques (mode capteur) avec le même matériau et d'autre part comme aucun contact physique n'est nécessaire entre le bobinage (créant le champ magnétique) et le matériau magnétostrictif, la commande peut se faire "à distance".
Mais l'effet magnétostrictif des matériaux utilisés à cette époque (principalement Al-Fe et nickel) était très faible. Vers 1950, les capteurs et transducteurs magnétostrictifs furent remplacés par des matériaux piézo-électriques devenus beaucoup plus performants.
Dans les années 1960 les recherches reprirent après l'étude prometteuse de Monsieur Belov à Moscou. Il étudiait la magnétostriction de certains métaux de la famille des terres rares. Puis Clark, un américain de la Naval Ordonnance Laboratory, découvrit en 1974 un alliage conservant, à température ambiante et sous un champ magnétique de 0.1 à 1 Tesla, une magnétostriction de l'ordre de 0.15% (1500 partie par million), ainsi naquit le terfenol-D (un alliage de dysprosium-terbium-fer). Le terme "magnétostriction géante" est souvent donné à ces nouveaux matériaux pour les distinguer de ceux de type Al-Fe ou nickel dont les effets magnétostrictifs sont moins importants. Le gain de ces matériaux à magnétostriction géante est d'environ de deux ordres de grandeurs, soit un facteur 100. Les performances en déformation sont environ deux fois plus importantes en comparaison avec les meilleurs matériaux piézo-électriques.
Depuis lors, les matériaux magnétostrictifs sont devenus compétitifs en terme de performance et prometteurs pour de nombreuses applications[13,Quandt] : le moteur magnétostrictif à onde ultrasonore, les capteurs, les actionneurs de forte puissance, le moteur Kiesewetter, le contrôle actif des vibrations, etc.
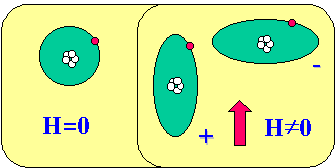
Nous allons nous intéresser tout d'abord à la magnétostriction à l'échelle microscopique afin de comprendre la source de ce phénomène. Nous définirons les particularités du nuage électronique de ces matériaux et le concept de direction de facile aimantation.
Le nuage électronique: L'énergie magnéto-élastique crée un couplage entre les déformations du réseau cristallin et l'état d'aimantation. La magnétostriction qui en résulte est la conséquence de la forme non sphérique du nuage électronique de valence de certains matériaux : lorsque le champ magnétique extrême fait tourner les moments magnétiques, le nuage électronique non sphérique tourne également et modifie l'équilibre cristallin en attirant ou en repoussant les ions voisins.
Direction de facile aimantation: le réseau cristallin impose des directions préférentielles pour l'aimantation. Néanmoins si un champ magnétique est appliqué au matériau, ses moments magnétiques auront tendance à s'aligner dans la direction de ce champ pour minimiser l'énergie interne. Il s'ensuit un réarrangement des domaines magnétiques, ce qui modifie les dimensions du réseau cristallin de l'échantillon, d'où la déformation de ses dimensions géométriques.
Les métaux et alliages magnétostrictifs sont naturellement cristallins. Cependant, sous certaines conditions et par des traitements spéciaux, il est possible de les fabriquer sous forme amorphe. Un des premiers modes de fabrication est la trempe de l'échantillon (c'est à dire un refroidissement brutal). Les atomes alors se figent et n'ont pas le temps de se réorganiser sous forme cristalline. Pour des raisons de transfert de chaleur, cette méthode ne peut être appliquée qu'à des matériaux de faibles volumes et épaisseurs (rubans, poudres...). Une seconde méthode consiste en des dépôts de couches minces afin de créer des couches de matériaux amorphes. Il n'est donc pas possible de trouver des barreaux magnétostrictifs amorphes. Par contre les couches magnétostrictives amorphes possèdent quelques avantages par rapport aux couches minces cristallines et c'est donc une des méthodes les plus intéressantes encore en pleine évolution en vue de leur utilisation dans des micro-systèmes[14,Betz].
Les principaux matériaux magnétostrictifs peuvent être séparés en deux groupes: les métaux (fer, cobalt, nickel principalement), les alliages métalliques et ferrites d'un coté et les composés de terres rares de l'autre.
C'est sur le nickel et sur les alliages métalliques que les premiers effets magnétostrictifs ont été observés. Mais ces matériaux ont une déformation très faible qui reste inférieure à 100 ppm avec des coefficients de couplage magnéto-mécanique[32,Berlincourt] de l'ordre de 0.3. Par contre leur température de Curie (voir Tableau II-1) est très élevée et garantit une bonne stabilité thermique.
Les ferrites ont ensuite été mis au point : leur effet magnétostrictif est plus important. Par ailleurs, ils peuvent être utilisés à des fréquences élevées et présentent un fort rendement électroacoustique. Leur inconvénient majeur est leur fragilité.
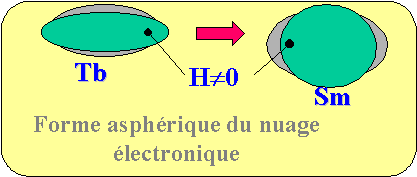
Pour parer aux problèmes liés aux très basses températures de curie (Tc) des terres rares, ces composés sont alliés à du fer dont la Tc est très élevée. Ainsi les composés TbFe2 et SmFe2 fournissent la plus grande magnétostriction (respectivement positive et négative) à température ambiante. Pour ces alliages le terme "magnétostriction géante" est utilisé. La température de curie de ces alliages reste faible et entraîne une variation des propriétés magnétostrictives de ces derniers avec la température. On montre que la magnétostriction décroît de façon monotone avec l'augmentation de la température.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En étudiant les résultats présentés (cf. Tableau II-1 ci-dessus), nous constatons que les coefficients magnétostrictifs des matériaux amorphes sont beaucoup plus faibles que ceux des matériaux polycristallins. Malgré cela les matériaux amorphes possèdent l'avantage d'avoir une déformation importante sous faible champ. De plus du fait de leur faisabilité en couche mince, ils conviennent parfaitement aux applications micro-systèmes[18,Body]. L'obtention de déformations significatives sous très faible champ est un aspect déterminant pour ces applications.
Les alliages polycristallins terre rare-Fe2 ont une température de Curie plus élevée que les matériaux amorphes mais ils souffrent d'une forte anisotropie qui gène le processus de rotation du champ. L'introduction de dysprosium permet d'adoucir le matériau en réduisant son énergie d'anisotropie tout en conservant une magnétostriction élevée.
Ce paragraphe décrit succinctement les différentes manifestations de la magnétostriction[19,Lee][20,Volluet][21,Bozorth]. Elles sont décrites dans le cas d'un barreau magnétostrictif soumis à un champ magnétique axial.
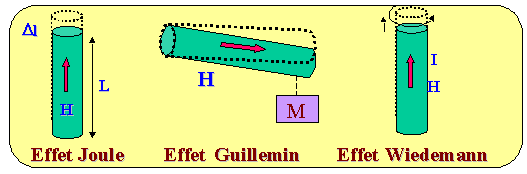
L'effet Joule longitudinal
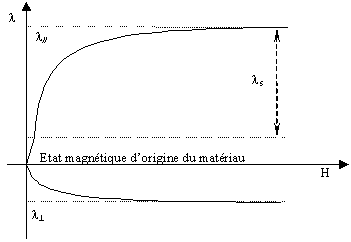
C'est le phénomène le plus important et le plus utilisé
de la magnétostriction. Il se caractérise par la variation
de la longueur D l d'un barreau magnétostrictif
de longueur l. Il est quantifié par le coefficient de magnétostriction
à saturation représentant la variation de la longueur du
barreau par rapport à son état désaimanté isotrope.
L'histoire magnétique du matériau est rarement connue. Pour
cette raison, nous considérons seulement la mesure différentielle
entre la magnétostriction parallèle et la magnétostriction
perpendiculaire à saturation :
|
|
Eq. 6
|
Ce coefficient peut prendre des valeurs positives (la magnétostriction positive) ou négatives (la magnétostriction négative) et permet la classification des matériaux magnétostrictifs en fonction de leur déformation (cf. Figure II-1).
L'effet Joule transversal
Il est lié à la variation des dimensions transversales du barreau qui accompagne son allongement élastique. Le coefficient de Poisson rend compte de cet effet transversal consécutif à un allongement.
L'effet Villari
Ce phénomène est l'effet longitudinal inverse. Lorsque la longueur du barreau est modifié mécaniquement, deux phénomènes sont possibles : soit le barreau s'aimante en créant un champ magnétique le long de son axe, soit son état d'aimantation se modifie. C'est le phénomène utilisé dans les capteurs magnétostrictifs de déformation.
L'effet Wiedemann
Cet effet consiste en une torsion du barreau suivant son axe lorsqu'il est traversé par un courant axial et aimanté selon son axe.
L'effet Guillemin ou effet de flexion
Un barreau suffisamment fin et long placé en position horizontale, encastré d'un coté avec un poids suspendu de l'autre coté subit une courbure. Lorsque ce barreau est traversé dans le sens de sa longueur par champ, le rayon de courbure varie. Cet effet met en évidence la dépendance des constantes de cisaillement du matériau avec le champ magnétique.
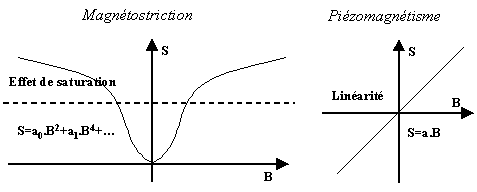
Les effets de variation de volume
L'effet de forme: variation de volume à champ faible, elle dépend de la géométrie de l'échantillon.
L'effet de cristal: Il se produit pour un champ magnétique plus élevé et devient plus important pour des valeurs très élevées du champ magnétique (c'est la magnétostriction forcée).
Cependant ces effets de variation de volume sont très faibles et comme nous l'avons déjà souligné (cf. II.1. La magnétostriction), l'effet magnétostrictif de joule est souvent considéré sans variation de volume (ce sera une de nos hypothèses pour la suite).
L'effet D E
La déformation cristalline entraîne une variation du module d'Young du matériau lorsque l'aimantation varie. La variation D E du module d'Young est l'une des causes du glissement de la fréquence de résonance des barreaux magnétostrictifs.
![]() est de l'ordre de 15% au maximum pour le Nickel mais peut atteindre jusqu'à
190% (à 200 kA/m) dans le cas du Terfenol-D [22,Savage].
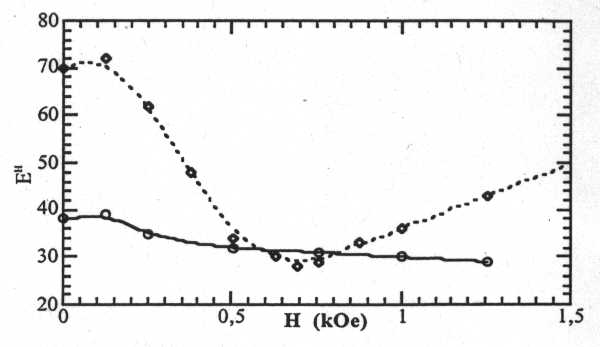
La Figure II-4 donne à titre d'exemple la courbe du module d'Young
à H constant pour deux alliages différents
[23,Clark].
est de l'ordre de 15% au maximum pour le Nickel mais peut atteindre jusqu'à
190% (à 200 kA/m) dans le cas du Terfenol-D [22,Savage].
La Figure II-4 donne à titre d'exemple la courbe du module d'Young
à H constant pour deux alliages différents
[23,Clark].
Nous retiendrons de cette énumération les effets principaux dont les applications industrielles sont directes : l'allongement longitudinal (Joule) et la compression transverse qui l'accompagne ainsi que la torsion (Wiedemann) du barreau.
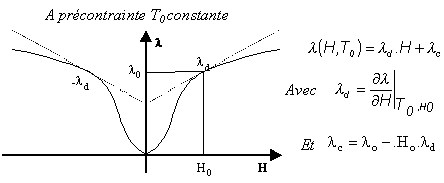
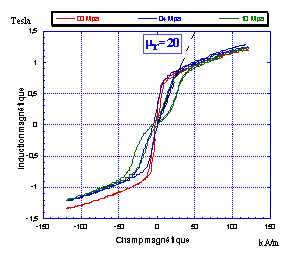
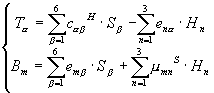 Contrainte et induction
magnétique
Contrainte et induction
magnétique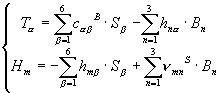 Contrainte et champ magnétique
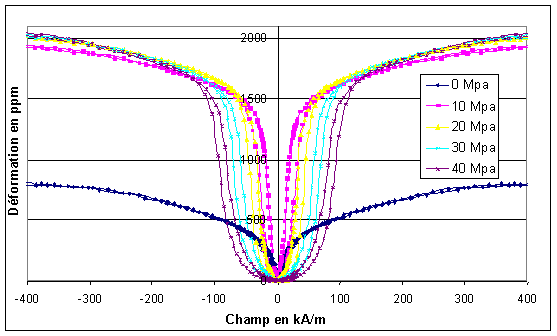
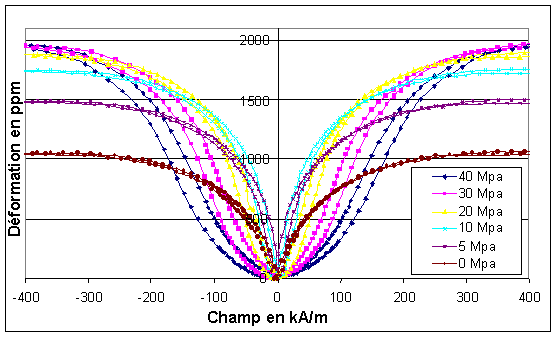
Contrainte et champ magnétique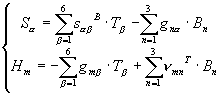 Déformation et
champ magnétique
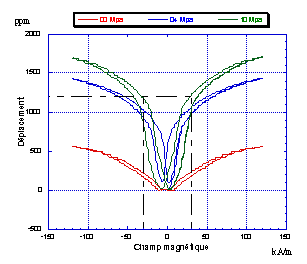
Déformation et
champ magnétique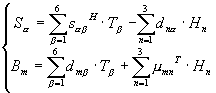 Déformation et
induction magnétique
Déformation et
induction magnétique